二叉树的反转意味着把树转换成它的镜像。简单地说，它是一棵树，所有非叶节点的左子节点和右子节点都被交换。

注意：叶节点也将互换。建议在继续处理此问题之前先学习顺序遍历和顺序后遍历。
让我们看一个二叉树的例子：

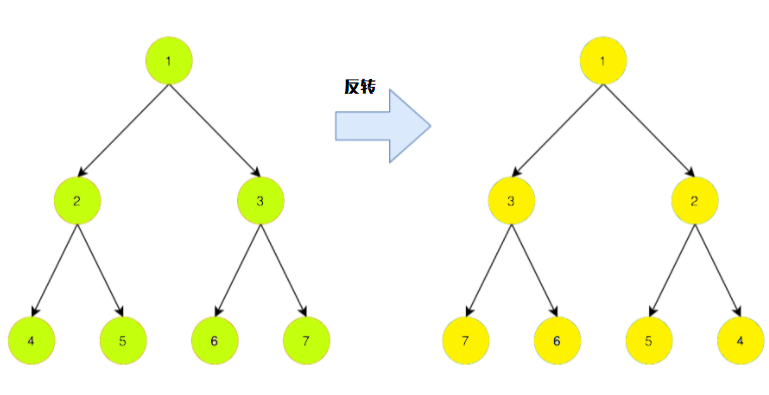
在上图中，我们看到了示例树及其反转或镜像版本。

方法一：递归方法

遵循以下步骤：
1、我们基本上从根开始对树进行后序遍历，首先遍历左子树，然后在处理根之前遍历右子树。
2、在处理每个节点的根节点时，如果它们的子节点不为null，则分别交换它们的左子节点和右子节点。
3、我们还检查给定的二叉树根是否为空。然后，我们继续相应地遍历左子树和右子树。如果我们在一个叶节点上，它没有任何子节点，我们返回null表示不需要交换。
4、为了验证树是否反转，我们在执行函数之前对树进行顺序遍历，然后在反转之后再次打印顺序遍历。您可以使用任何遍历算法来验证输出。
现在，让我们看看以上代码的实现：

 //Class containing attributes of each node of tree
class Node 
{ 
    int data; 
    Node left, right; 
  
    Node(int data) 
    { 
        this.data = data; 
        left = null;
        right = null; 
    } 
} 
  
class Tree 
{ 
    Node root; 
  
    void invertTree(Node node) 
    { 
        if (node == null) 
            return; 
  
        //we call or recur for left subtrees then the right subtrees
        invertTree(node.left); 
        invertTree(node.right); 
  
        //swap the left and right child of each non-leaf node*/
        Node temp=node.left;
        node.left = node.right; 
        node.right = temp; 
  
    } 
  
  
    /* Helper function to test invertTree() by printing In-Order traversal*/
    void printInOrder(Node node) 
    { 
        if (node == null) 
            return; 
  
        printInOrder(node.left); 
        
        System.out.print(node.data + " "); 
  
        printInOrder(node.right); 
    } 
  
    /*Driver code to test for sample tree*/
    public static void main(String args[]) 
    { 
        /* creating a binary tree and entering the nodes */
        Tree tree = new Tree(); 
        tree.root = new Node(20); 
        tree.root.left = new Node(10); 
        tree.root.left.left = new Node(5); 
        tree.root.left.right = new Node(15); 
        tree.root.right = new Node(30);
        tree.root.right.left = new Node(25);
        tree.root.right.right = new Node(35);
  
        /* print inorder traversal of the input tree */
        System.out.println("Inorder traversal of Input Tree is :"); 
        tree.printInOrder(tree.root); 
        System.out.println();
        
        
        System.out.println(); 
        /* convert tree to its mirror */
        tree.invertTree(tree.root); 
  
        /* Inorder traversal of the Inverted Binary tree */
        System.out.println("Inorder traversal of Inverted Tree is : "); 
        tree.printInOrder(tree.root); 
  
    } 
} 

输出

 Inorder traversal of Input Tree is :
5 10 15 20 25 30 35 
 
Inorder traversal of Inverted Tree is : 
35 30 25 20 15 10 5

方法二：迭代的方法 

其主要思想是使用队列对树进行水平顺序遍历。我们首先将根放入队列。当我们遍历特定级别上的所有节点时，我们交换每个节点的左子节点和右子节点。在此之后，我们将当前节点的左、右子节点添加到队列中，以继续级别顺序遍历。
最后，我们打印顺序遍历树来验证倒树。
让我们看一下实现：

 // import the Queue interface of Collections implemented using Linked List
import java.util.Queue;
import java.util.LinkedList;
//Class for each node of tree
class Node 
{ 
    int data; 
    Node left, right; 
  
    Node(int data) 
    { 
        this.data = data; 
        left = null;
        right = null; 
    } 
} 
  
class Tree 
{ 
    Node root; 
  
    void invertTreeIterative(Node root) 
    { 
        if (root == null) 
        return; 
  
        Queue<Node> queue = new LinkedList<>(); 
        //Add root first
        queue.add(root); 
      
        //We do level order traversal 
        while (queue.size() > 0) 
        { 
            // Get node of each level 
            Node curr = queue.poll();
      
            // swap left child with right child 
            Node temp = curr.left; 
            curr.left = curr.right; 
            curr.right = temp;; 
      
            // enqueue left and right child 
            if (curr.left != null) 
                queue.add(curr.left); 
            if (curr.right != null) 
                queue.add(curr.right); 
        } 
      
    } 
  
    /* Helper function to test invertTree() by printing In-Order traversal*/
    void printInOrder(Node node) 
    { 
        if (node == null) 
            return; 
  
        printInOrder(node.left); 
        
        System.out.print(node.data + " "); 
  
        printInOrder(node.right); 
    } 
  
    /*Driver code to test for sample tree*/
    public static void main(String args[]) 
    { 
        /* creating a binary tree and entering the nodes */
        Tree tree = new Tree(); 
        tree.root = new Node(20); 
        tree.root.left = new Node(10); 
        tree.root.left.left = new Node(5); 
        tree.root.left.right = new Node(15); 
        tree.root.right = new Node(30);
        tree.root.right.left = new Node(25);
        tree.root.right.right = new Node(35);
  
        /* print inorder traversal of the input tree */
        System.out.println("Inorder traversal of Input Tree is :"); 
        tree.printInOrder(tree.root); 
        System.out.println();
        
        
        System.out.println(); 
        
        /* convert tree to its mirror */
        tree.invertTreeIterative(tree.root); 
  
        /* Inorder traversal of the Inverted Binary tree */
        System.out.println("Inorder traversal of Inverted Tree is : "); 
        tree.printInOrder(tree.root); 
  
    } 
}

 输入树的顺序遍历为：

5 10 15 20 25 30 35

倒树的顺序遍历为：

35 30 25 20 15 10 5

时间复杂度：与递归方法相同，遍历树的所有节点时需要O（n）时间。
空间复杂度：我们使用一个队列来存储执行期间的所有节点，因此复杂度为O（n）。

对于本文，您可以尝试执行上述代码。请随时在评论部分询问您的问题。

原文：Invert a Binary Tree – Recursive and Iterative Approach in Java